[Python] DFS/BFS : 프로그래머스 LV.3 퍼즐 조각 채우기

문제 링크 

프로그래머스

문제 설명 

첫 번째로 solution함수가 실행되면서 주어진 game_board와 table을 이용하여 문제를 해결해 나간다. 우선적으로 visited_g, visited_t라는 방문처리를 나타내는 맵을 아래와 같이 만들어준다.

테이블들을 순회하면서 빈 공간과 퍼즐들을 찾게 되는데, 이때 bfs함수를 이용하여 현재좌표를 기준으로 상,하,좌,우 칸들을 탐색하여 연결된 좌표들을 찾는다.

bfs함수가 모두 완료되면, 위와 같이 block_t, empty_g 테이블이 완성된다. 여기서 중요한 아이디어가 나온다, 처음에 이 부분을 생각하지 못하여 다른 풀이들을 참조하고 배웠다. 사람은 동일한 모양의 퍼즐을 단번에 인지할 수 있지만, 컴퓨터는 동일한 모양이어도 다른 위치(좌표)에 있으면 같은 퍼즐이라고 판단하지 않는다. 이것의 해결 방법은 비교하는 테이블들을 모두 같은 위치로 정규화시키는 것이다. 

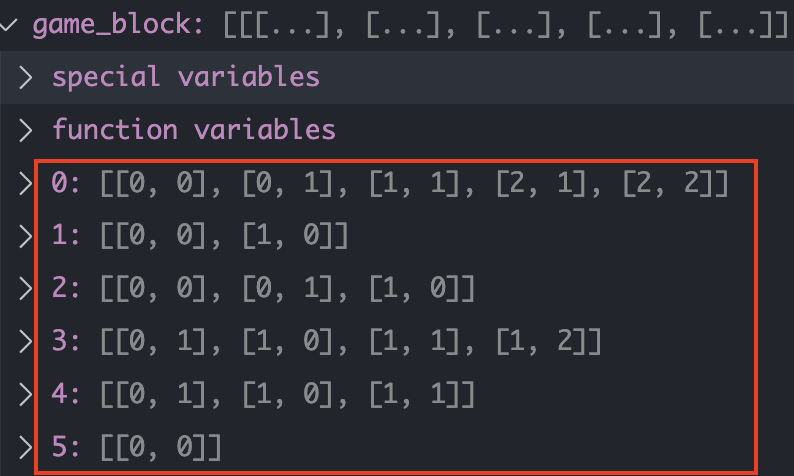
위와 같이 standard 함수를 통해 정규화 시킨 테이블들을 만들어 주었다.

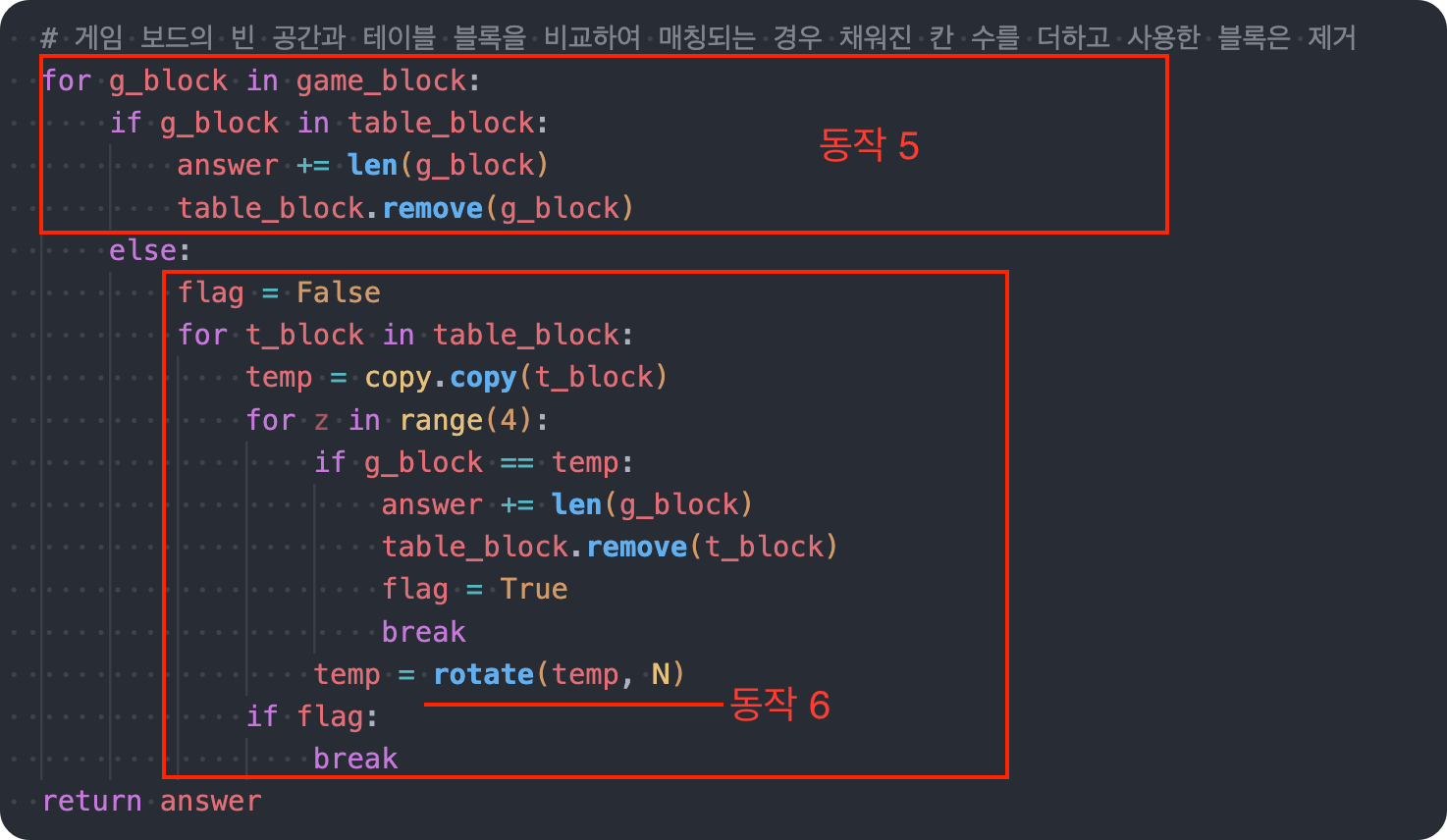
마지막으로, 두개의 테이블을 비교하면서 매칭시키고, 주어진 조건에 따라 퍼즐은 90도 회전이 가능하기 때문에 매칭이 안된 블록들 중 회전했을 때 매칭되는 경우를 확인하기 위해 rotate함수를 이용해 퍼즐 조각을 회전시키면서 매칭해 보고, 매칭이 된다면 answer값을 1씩 올려주면서 끝이 난다. 

전체 코드 

# <필요로직>
# 맵을 만드는 로직
# 게임보드랑 퍼즐테이블의 상태를 나타내는 로직
# 상하좌우 이동하는 로직
# 회전 로직
# 게임보드 퍼즐테이블 비교하면서 맞춰보는 로직

from collections import deque
import copy

# 상, 하, 좌, 우 방향 이동을 위한 상대 좌표
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
empty_g = []  # 빈 공간 정보를 저장할 리스트
block_t = []  # 테이블 위의 블록 정보를 저장할 리스트

# 너비 우선 탐색(BFS)을 사용하여 연결된 공간을 찾는 함수
def bfs(x, y, N, visited, array, check):
    space = []  # 연결된 공간의 좌표를 저장할 리스트
    que = deque()
    que.append([x, y])
    space.append([x, y])
    visited[x][y] = True #방문처리하기
    # 정확히 이해가 필요한 동작부분
    while que:
        px, py = que.popleft()
        for i in range(4): #상,하,좌,우 방향 탐색하기
            nx = px + dx[i] #현재좌표에서 이동한 새로운 좌표 구하기
            ny = py + dy[i]
            if nx < 0 or ny < 0 or nx >= N or ny >= N: # 새로 계산한 좌표가 게임보드의 범위를 벗어나면 무시하고 다음 방향 진행하기
                continue
            if visited[nx][ny] is False and array[nx][ny] == check: # 새로운 좌표가 아직 방문하지 않았고, array값이 check와 같다면
                visited[nx][ny] = True #새로운 좌표도 방문처리
                que.append([nx, ny]) #새로운 좌표를 다음 탐색 대상으로 큐에추가
                space.append([nx, ny])# 연결된 좌표칸을 저장

    return sorted(space)

# 퍼즐 조각을 90도 회전시키는 함수
def rotate(b, N):
    new_board = []
    for block in b:
        new_board.append([block[1], N - 1 - block[0]]) # -> 회전 핵심 공식! 
    return sorted(standard(new_board, N))

# 퍼즐 조각의 좌표를 정규화하는 함수(조각을 좌측상단을 모두 이동시키기)
def standard(b, N):
    change = []
    #가장 작은 x,y값을 N으로 초기 세팅
    minx = N 
    miny = N

    for i in b:
        #현재 퍼즐조각내의 최소 x,y값 찾기
        minx = min(minx, i[0])
        miny = min(miny, i[1])
    for x, y in b:
        # 현재 좌표에서 최소x,y빼고 change리스트에 추가
        change.append([x - minx, y - miny])
    return sorted(change)

# 게임 보드와 테이블에서 퍼즐 조각을 찾아 총 몇 칸을 채울 수 있는지 계산하는 함수
def solution(game_board, table):
    global answer  # 정답을 저장하기 위한 전역 변수
    answer = 0
    N = len(game_board)

    # 게임 보드와 테이블의 방문 여부를 기록할 2차원 배열 초기화
    visited_g = [[False for _ in range(N)] for _ in range(N)]
    visited_t = [[False for _ in range(N)] for _ in range(N)]

    # 게임 보드와 테이블을 순회하면서 빈 공간과 블록을 찾아서 리스트에 저장
    for i in range(N):
        for j in range(N):
            if game_board[i][j] == 0 and visited_g[i][j] is False: #빈공간과 방문하지않은 칸
                empty_g.append(bfs(i, j, N, visited_g, game_board, 0))
            if table[i][j] == 1 and visited_t[i][j] is False: # 도형(채워져있는칸)과 방문하지 않은 칸
                block_t.append(bfs(i, j, N, visited_t, table, 1))
            else:
                continue

    table_block = []  # 테이블 블록 정보를 저장할 리스트
    for a in block_t:
        table_block.append(standard(a, N))

    game_block = []  # 게임 보드의 빈 공간 정보를 저장할 리스트
    for b in empty_g:
        game_block.append(standard(b, N))

    # 게임 보드의 빈 공간과 테이블 블록을 비교하여 매칭되는 경우 채워진 칸 수를 더하고 사용한 블록은 제거
    for g_block in game_block:
        if g_block in table_block:
            answer += len(g_block)
            table_block.remove(g_block)
        else:
            flag = False
            for t_block in table_block:
                temp = copy.copy(t_block)
                for z in range(4):
                    if g_block == temp:
                        answer += len(g_block)
                        table_block.remove(t_block)
                        flag = True
                        break
                    temp = rotate(temp, N)
                if flag:
                    break
    return answer